Symbolic Model Discovery

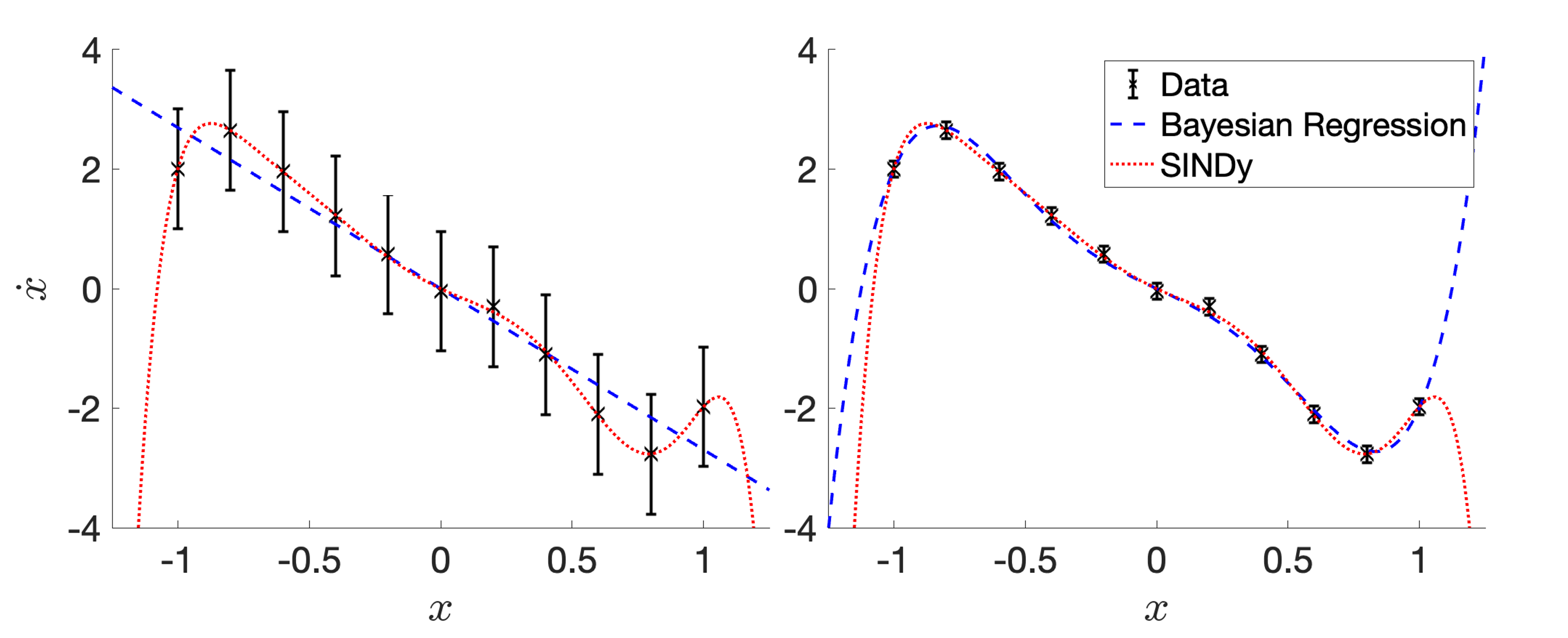
The Bayesian Identification of Nonlinear Dynamics (BINDy) framework is the next iteration of the popular SINDy framework for learning equations from data. By proper treatment of the noise in the data through the reformulation of the model discovery problem in the Bayesian framework, BINDy has shown major improvement in noise robustness and data efficiency in the learning problem. It also invited more mathematically rigorous treatment of the SINDy framework and found the field on a firmer foundation.

Our first work (Fung et al., 2025) on BINDy has illustrated the importance and rigour of interpreting the model selection problem in the Bayesian sense. By exploiting linear regression the same way SINDy has and using Laplace approximation, our algorithm is almost as fast as the original SINDy, while being more noise robust.

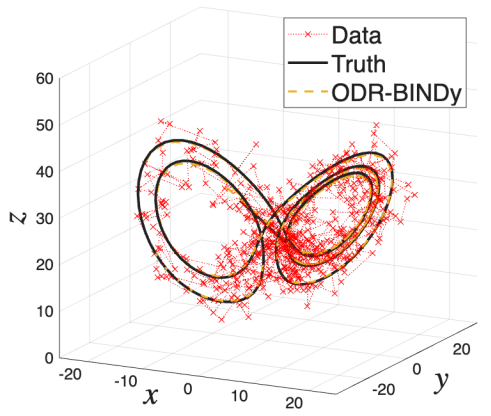
Our second go at the framework (Fung, 2025) focus more in cases when measurement noise is large enough to distort noise propagation through the nonlinear library. We showed that in those cases, the noise model should include both noise in measurments and noise in the model arising from numerical trucation or stohcasticity. By explioting information from neighbouring time-points and through nonlinear optimisation, our ODR-BINDy algorithm can denoise the data, perform parameter estimation and select the most parsimonious model at the same time. In our benchmark, ODR-BINDy outperforms all existing methods in noise robustness and data requirements.

Success Rate of recovering Lorenz63 from data using different SINDy derivatives

Want to give our algorithm a try? Why not check out our MATLAB applet designed for 2D/3D time-series data?

References

2025

RSPA

Rapid Bayesian identification of sparse nonlinear dynamics from scarce and noisy data

Lloyd Fung, Urban Fasel, and Matthew Juniper

Proc. R. Soc. A. Paper for the software package B-SINDy , Feb 2025

Abs DOI

We propose a fast probabilistic framework for identifying differential equations governing the dynamics of observed data. We recast the sparse identification of nonlinear dynamics (SINDy) method within a Bayesian framework and use Gaussian approximations for the prior and likelihood to speed up computation. The resulting method, Bayesian-SINDy, not only quantifies uncertainty in the parameters estimated but also is more robust when learning the correct model from limited and noisy data. Using both synthetic and real-life examples such as lynx–hare population dynamics, we demonstrate the effectiveness of the new framework in learning correct model equations and compare its computational and data efficiency with existing methods. Because Bayesian-SINDy can quickly assimilate data and is robust against noise, it is particularly suitable for biological data and real-time system identification in control. Its probabilistic framework also enables the calculation of information entropy, laying the foundation for an active learning strategy.
Overcoming error-in-variable problem in data-driven model discovery by orthogonal distance regression

Lloyd Fung

Paper for the software package ODR-BINDy , Feb 2025

DOI arXiv